A minimal "push-pull" bistability model explains oscillations between quiescent and proliferative cell states.
Posted on: 9 July 2018 , updated on: 18 July 2018
Preprint posted on 26 June 2018
Article now published in Molecular Biology of the Cell at http://dx.doi.org/10.1091/mbc.E18-01-0017
How do cells decide when to grow and divide? Resource availability, cell history, and neighboring cell state drive oscillations between quiescence and proliferation.
Selected by Lauren NevesCategories: systems biology
Background
Quiescence is the predominant state of the majority of eukaryotic cells. Quiescence, sometimes termed G0, is a reversible dormant state in which cells are non-proliferative but can return to active growth and division at a later time. This ability to enter and exit the cell cycle is critically important for tissue homeostasis as well as response to injury and environmental perturbations. This is particularly apparent in adult mammalian stem cells that must proliferate episodically and in response to damage throughout the lifespan of the animal.
However, deciding factors that drive transitions between quiescence and active growth are not well understood. Intriguingly, in many organisms, cell states are heterogeneous within a genetically identical population present in the same environment. Such heterogeneity of the transition between growth and quiescence can be clearly observed in studies of yeast metabolic cycles (YMC), in which yeast populations are driven to oscillating cell states by nutrient-limitation. Although cells are genetically identical, only a subpopulation of cells proliferates during each oscillation.
What makes some quiescent cells more competent for re-entry in to the cell cycle than others? A number of studies suggest that differences in internal metabolic states help condition cells to respond to environmental cues. A recent paper by Dr. Sandeep Krishna and Dr. Sunil Laxman build a model to describe transitions between growth and quiescence in yeast populations. This model reveals that oscillations must rely on resource (nutrient) availability, communication between dormant and active cells, and cell state history. Additionally, they suggest that two key internal metabolites are sufficient to drive oscillatory behavior.
Key Findings
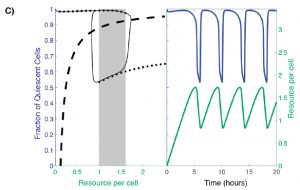
Analysis of existing data from YMC studies revealed oscillation between two distinct equilibrium states under nutrient-limiting conditions: quiescence (Q) and growth (G). In order to capture this two-state population, the authors build a model that considers: (1) the availability of some necessary resource and (2) the fraction of Q cells (Figure 2C, dotted line). In such a model, at low resource availability, the majority of cells within the population are quiescent, while at high resource availability a large subpopulation of cells are proliferative. However, there is a range of resource availability in which the system becomes bistable: two stable cell population states are possible. In this range, the fraction of Q versus G cells may be high or low (Figure 2C, shaded box).
Figure 2C from the preprint: A hysteretic oscillator, based on switching between Q and G states, a required communication between Q, G and the resource, and the oscillation of the amounts of resource itself that controls the Q<->G transitions. In the left panel: The thin black curve shows the path traced by the oscillation in the q-a plane, the thick dashed line is the curve along which production of resource exactly balances consumption/dilution, and the solid black dots trace the high and low branches of the steady state [fraction of quiescent cells] levels when the resource level is held constant (the grey rectangle indicates the region of bistability). In the right panel: blue and green curves show, respectively, the fraction of quiescent cells and the resource level as a function of time.
The authors argue that the possible steady state fraction of Q cells in the bistable region depends on the systems “memory”. When resource availability remains fixed, the steady state fraction of Q cells in a population ultimately depends on where the population started. As in Figure 2C, a population of cells that begins to the right of the shaded box at a high nutrient level begins with a low fraction of Q cells and will therefore settle at a lower Q cell fraction when it reaches the bistable region/shaded box. However, if resource availability is variable, as is the case when growing cells actively consume the resource, oscillations between Q and G states occur as the cell population is driven to the edges of the bistable region (Figure 2C, right panel). This oscillatory behavior implies that cells from either cell state must be able to communicate within the population and/or sense cell density changes. The authors propose that there must be a mechanism in which cells are capable of influencing neighboring cells to either remain in, or transition to, their current state. Q cells “pull” G cells to transition to the quiescent state and “push” other Q cells to remain quiescent (and vise versa).
Furthermore, by altering the speed at which cells switch between quiescent and growth states (transition rate), the authors show that their model can generate a diverse set of oscillation patterns. In fact, this model recapitulates a wide range of oscillations experimentally observed in variant yeast strains, indicating that this model may be relevant for many cell types.
Finally, the authors show that availability of acetyl CoA and NADPH, two key internal metabolites, are sufficient to drive oscillatory behavior in models. Supplying cells with excess acetyl CoA in the model drives transition to proliferation, reflecting experimentally observed data using excess external nutrients (such as glucose) (Figure 5C).
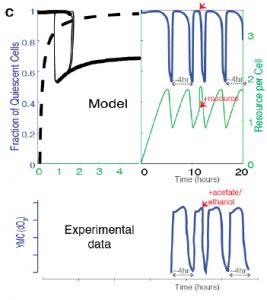
Figure 5C from the preprint: Predicted effect on the oscillation waveforms and the Q and G states, when a bolus of the resource is added to cells in the Q state vs experimentally observed data on oxygen consumption when a resource, acetate (the trace is similar with for resources like ethanol, acetate, acetaldehyde, glucose) is added to cells in the low oxygen consumption phase.
This model suggests that specific metabolites may be responsible for initiation of oscillations in vivo. Variations in metabolite accumulation among cells could establish cell state memory and drive differences in individual cell state transitions.
Thoughts and Future Directions
There is an increasing trend toward interdisciplinary approaches in answering biological questions. In this paper, the authors attempt to describe a critical biological cycle in mathematical terms to quantify the contribution of specific factors in its regulation. I have found that, while these approaches may not be able to sufficiently answer mechanistic questions (for example, how do quiescent and proliferative cells communicate?), they can help frame and focus future questions and hypotheses.
Some questions I have:
- The authors show that transition rate alters oscillation pattern. What factors determine transition rate, and can these be used to predict transition rates for different cell types?
- The ability to oscillate between dormant and active growth is required for many biological processes, such as immune response and wound healing, and is central to many disorders, including muscular dystrophy and cancer. As acetyl CoA and NADPH are key drivers of growth-quiescence oscillations, can factors that affect availability of these metabolites be used to manipulate cell fate decisions and potentially be used for therapeutic purposes?
Further reading
- Dhawan, J., and Laxman, S. (2015). Decoding the stem cell quiescence cycle – lessons from yeast for regenerative biology. J. Cell Sci. 128, 4467–4474.
- Coller, H. (2011). The Essence of Quiescence. Science. 335(6059): 1074-1075
Sign up to customise the site to your preferences and to receive alerts
Register hereAlso in the systems biology category:
Modular control of time and space during vertebrate axis segmentation
AND
Natural genetic variation quantitatively regulates heart rate and dimension
Girish Kale, Jennifer Ann Black
Expressive modeling and fast simulation for dynamic compartments
Benjamin Dominik Maier
Clusters of lineage-specific genes are anchored by ZNF274 in repressive perinucleolar compartments
Silvia Carvalho
preLists in the systems biology category:
‘In preprints’ from Development 2022-2023
A list of the preprints featured in Development's 'In preprints' articles between 2022-2023
| List by | Alex Eve, Katherine Brown |
EMBL Synthetic Morphogenesis: From Gene Circuits to Tissue Architecture (2021)
A list of preprints mentioned at the #EESmorphoG virtual meeting in 2021.
| List by | Alex Eve |
Single Cell Biology 2020
A list of preprints mentioned at the Wellcome Genome Campus Single Cell Biology 2020 meeting.
| List by | Alex Eve |
ASCB EMBO Annual Meeting 2019
A collection of preprints presented at the 2019 ASCB EMBO Meeting in Washington, DC (December 7-11)
| List by | Madhuja Samaddar et al. |
EMBL Seeing is Believing – Imaging the Molecular Processes of Life
Preprints discussed at the 2019 edition of Seeing is Believing, at EMBL Heidelberg from the 9th-12th October 2019
| List by | Dey Lab |
Pattern formation during development
The aim of this preList is to integrate results about the mechanisms that govern patterning during development, from genes implicated in the processes to theoritical models of pattern formation in nature.
| List by | Alexa Sadier |









 (No Ratings Yet)
(No Ratings Yet)