Holimap: an accurate and efficient method for solving stochastic gene network dynamics
Posted on: 25 March 2024 , updated on: 15 August 2024
Preprint posted on 28 February 2024
Article now published in Nature Communication at https://doi.org/10.1038/s41467-024-50716-z
Breaking the curse of dimensionality: Chen Jia and Ramon Grima propose an efficient framework that accurately predicts stochastic time-dependent protein dynamics.
Selected by Benjamin Dominik MaierCategories: bioinformatics, systems biology
Updated 15 August 2024 with a postLight by Benjamin Dominik Maier
Congratulations to Chen Jia and Ramon Grima! Their manuscript has now been published in Nature Communications (link to the journal article). The manuscript has been reviewed by 5 reviewers (2 of them as part of Nature’s early career co-reviewing initiative, yeah) and the review history can be found here.
Based on a reviewer suggestion, a new section has been added to showcase the generalization of Holimap to networks with post-translational or post-transcriptional regulation with complex protein-protein, protein-RNA, and RNA-RNA interactions. Moreover, the authors added a proof of Holimap’s computational cost for general networks as well as a quantification of the numerical stability of 2-HM and 4-HM. Additionally, the authors made textual changes to make the paper more accessible for a broader audience, including e.g. a more comprehensive introduction of SSA and FSP, reasoning of the biological relevance of some parameters, a flowchart of Holimap with a step-to-step guide, a systematic comparison with neural network-based approaches, and an outline of which Holimap version should be used in different scenarios.
In the author’s response to the reviewer comments, the authors hint that they are planning to extend their existing MomentClosure.jl software package (article | github) to incorporate their new Holimap methodology, which they plan to release within the next year.
Personal Perspective/Background
Whenever I simulate mathematical models, I have to decide between a deterministic, stochastic or hybrid simulation routine. Deterministic models are completely predictable, meaning that for a given set of inputs, the model will always result in the same set of outputs. Although sufficient for large reacting molecule numbers and stable systems, they cannot resolve dynamics of (small) populations or expression distributions, which are crucial for understanding differences between species, cell types, and states. In contrast, stochastic simulations model individual molecular interactions and reactions probabilistically, treating genes and proteins as individual (discrete) molecules rather than averaged (continuous) concentrations. While they account for stochasticity and provide insights into expression patterns (e.g. unimodal vs bimodal), they can become computationally expensive due to the need for simulating numerous trajectories to fully capture the system dynamics (Fig. 1).
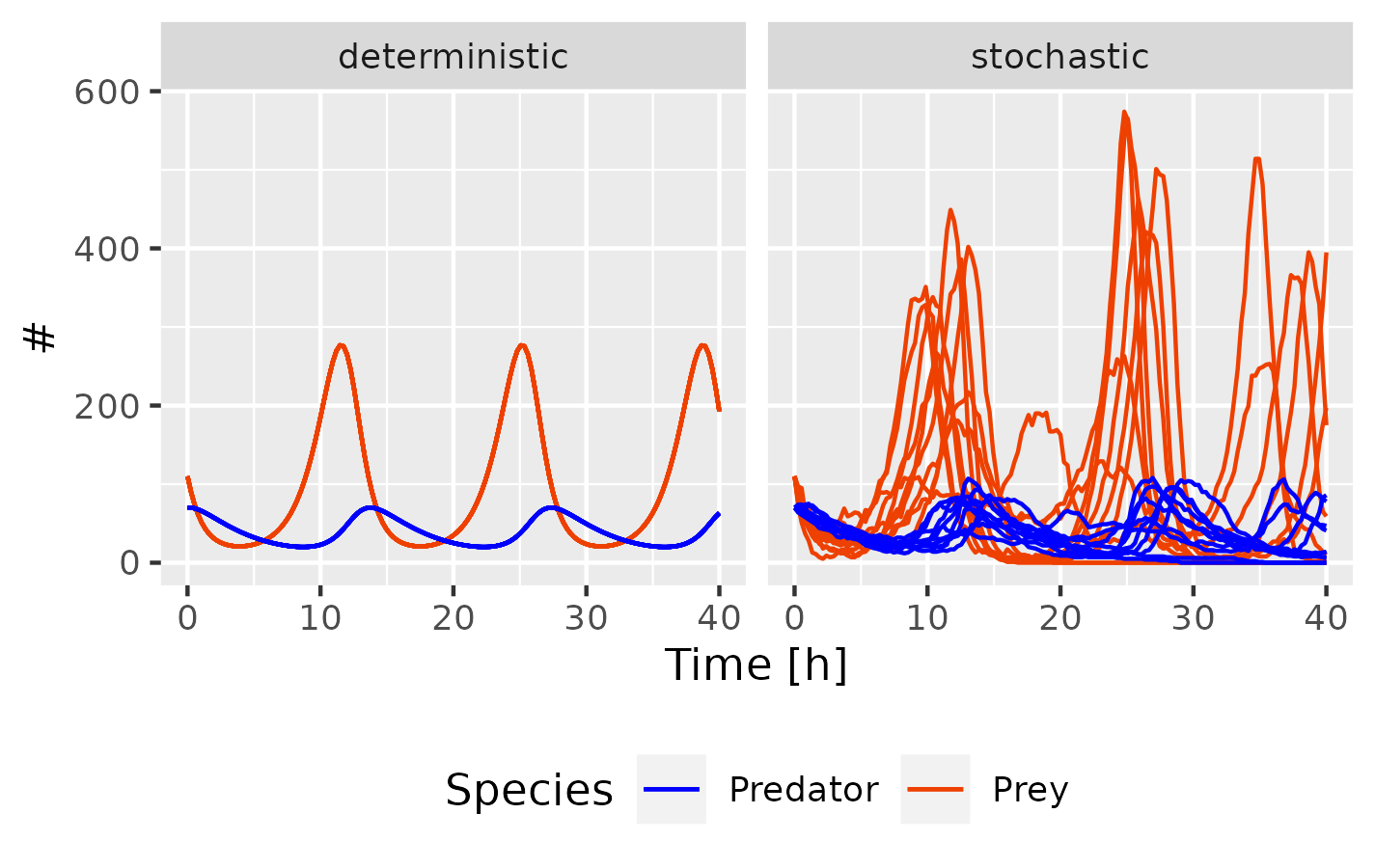
Fig. 1 Lotka-Volterra System. Comparison of deterministic (LSODA) and stochastic (adaptive SSA/τ-leap) simu- lations (10 trajectories) for a mathematical model of inter- specific competition in COPASI. The model consists of 4 reactions (prey growth, predation, predator growth, predator death) and displays a periodic activity.
(One might say that deterministic simulations are similar to bulk sequencing while stochastic simulations are comparable to the more fancy and expensive single cell sequencing.)
Stochastic Protein Dynamics
Stochasticity is an inherent property of biological systems which ensures that a system is simultaneously robust enough to function reliably while maintaining adaptability to dynamic environmental changes. Stochasticity arises from the probabilistic nature of molecular processes like transcriptional bursting (intrinsic noise), cell-to-cell variations (extrinsic noise) as well as technical variability introduced by experimental protocols.
Finite State Projection (FSP) and Stochastic Simulation Algorithm (SSA)
Biological systems can be described using stochastic chemical master equations (CME) to mathematically model how a system and its molecules evolve over (continuous) time. The clever thing about these equations is that they are memoryless, meaning that future states depend solely on the present state and not the past sequence of events (Markov property). The solution of the CME is the probability distribution of all possible system states, yet solving it is challenging as a) many systems have infinite states and b) computational complexity increases exponentially with species numbers (“curse of dimensionality”).
If the behaviour of a system can be represented by a finite set of states and transitions between them, applying Finite State Projection (FSP) (Munsky & Khammash, 2006) can model it as a Markov chain. The master equation of the Markov chain can then be solved analytically to compute the probability distribution of the system’s state at any given time.
However, for large and complex reaction networks, analytical solutions like FSP may not be feasible. Monte Carlo simulation-based algorithms such as the Doob-Gillespie/Stochastic Simulation Algorithm (SSA) use random sampling to obtain approximative numerical results (used for Figure 1). SSA simulates the systems dynamics by iteratively selecting both the time until the next event as well as the specific event to occur (Gillespie, 1976). SSA can be further sped up using time-leaping (e.g., τ-leap) and/or system-partitioning methods.
More thorough mathematical explanations of all these concepts can be found in Dinh & Sidhe (2016).
Key Findings
Overview
Gene regulatory networks (GRNs) represent genes and transcription factors (TF) that interact with each other to regulate the expression of genes within a cell. As a TF may activate or repress the expression of multiple target genes, and a gene may be regulated by multiple transcription factors, understanding their dynamics is challenging.
In this featured preprint, Jia and Grima developed a High-Order LInear-Mapping APproximation framework (HOLIMAP) to accurately and efficiently predict stochastic time-dependent protein dynamics. Its core idea is to decouple the complex gene-gene interactions from the nonlinear GRN and transform them into a linear network with a much smaller state space, which can then be analytically solved using FSP. This not only significantly reduces the CPU time compared to approximating the non-linear model with SSA simulations but also yields smoother distributions given a lower approximation error.
HOLIMAP is based on their previously published linear-mapping approximation (LMA) framework (Cao & Grima, 2018), in which the protein binding rates were substituted by effective gene switching rates to transform the higher-order gene-protein reactions into much simpler effective linear first-order reactions. HOLIMAP goes one step further by also substituting the unbinding rates (2-parameter Holimap) and additionally the protein burst frequencies (4-parameter Holimap). The difficulty of finding the right effective parameters for the mapping hereby scales with the number of moment equations that need to be computed and is hence dependent on the cooperativity of the system. Cooperativity happens when there are synergistic effects from seemingly independent components of a system, like oxygen binding to haemoglobin. In transcriptional regulation cooperativity occurs e.g. due to the binding of a TF to a DNA binding site enhancing the binding of other TF to adjacent sites.
Key Finding I: Benchmarking LMA and Holimap
Next, the authors evaluated the accuracy of LMA and Holimap in estimating steady-state protein distributions by benchmarking them against a nonlinear system solved with FSP. The steady-state protein distributions were quantified using the Hellinger distance (HD), a bounded metric (0 to 1) for probability distributions over a given space. Holimap outperforms LMA in all conditions with an overall 3.5x lower Hellinger distance. The authors showed that 2-HM and 4-HM can efficiently capture bimodality and its approximation error does not increase with higher cooperativity (Fig. 2A). Moreover the authors demonstrated that Holimap not only accurately predicts steady state conditions, but also performs well estimating the time evolution of protein distributions.
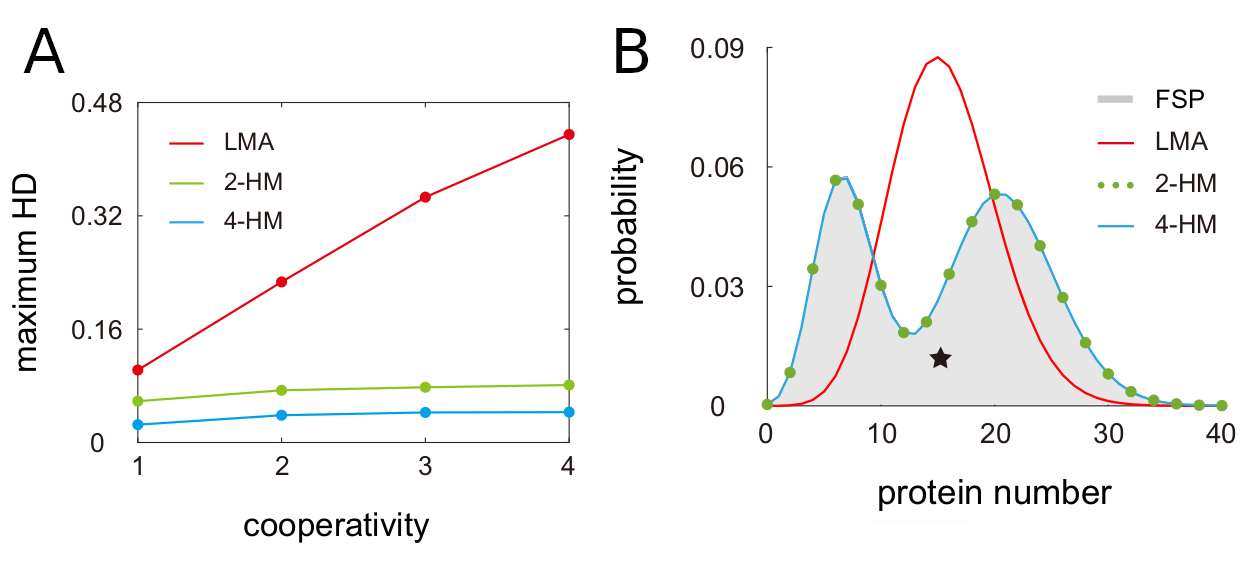
Fig. 2 Benchmark of LMA and Holimap using the Hellinger Distance. a) Effect of cooperativity on Hellinger Distance. b) Bimodality of a steady-state two-node gene network. Figure taken from Jia and Grima (2024), BioRxiv published under the CC-BY-NC-ND 4.0 International licence.
Key Finding II: Mechanisms of Bimodality
Bimodal protein distributions usually originate from either a positive feedback loop with ultra-sensitivity (type-I) or slow switching between gene states (type-II). Interestingly, when exploring two node networks, the authors identified bimodality in systems which do not fulfil any of these criterias. Instead their newly identified type-III bimodality occurred for small binding rates of one interaction partner and a high one from the other binding partner. Again, this bimodality was only captured by Holimap but missed completely by LMA (Fig. 2B). Similarly, for three-node networks with deterministic oscillations, Holimap is able to capture them while LMA cannot resolve the oscillations.
Key Finding III: Hybrid combination of SSA and Holimap
An ideal stochastic simulation method would be simultaneously efficient (fast & scalable) when computing (large) systems while yielding smooth and accurate distributions of the population dynamics over time. To address this, Jia and Grima developed a hybrid SSA + Holimap framework (Fig. 3).
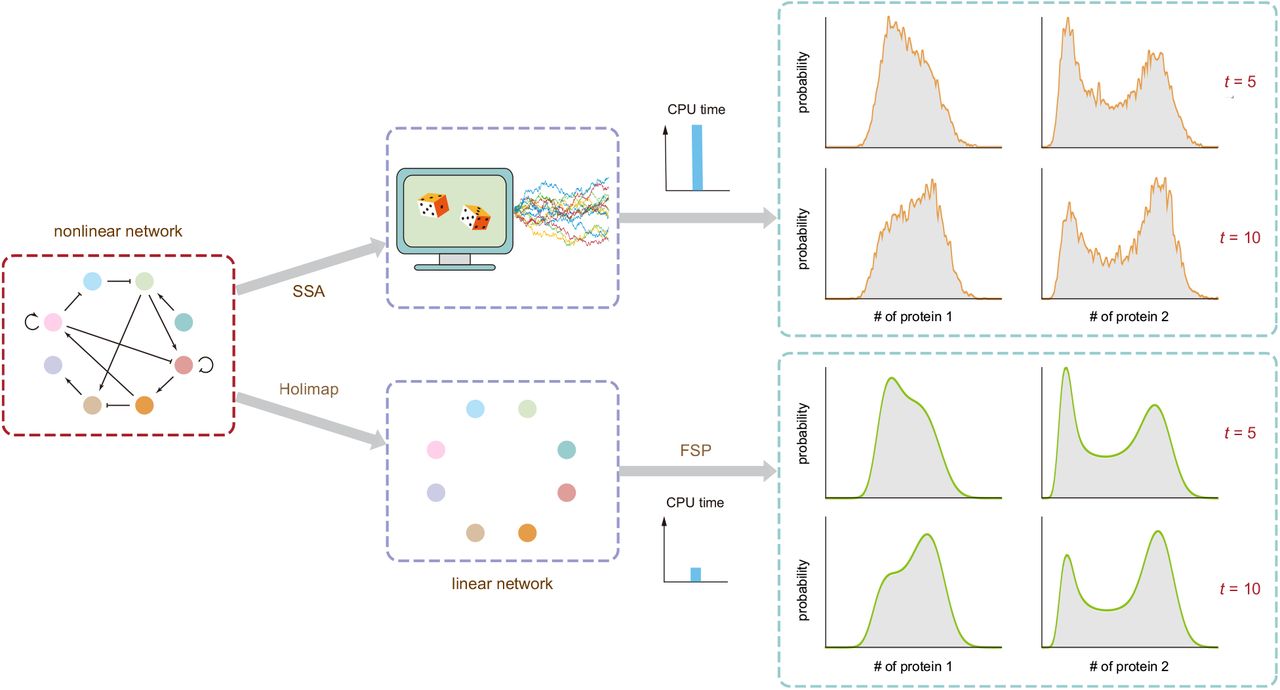
Fig. 3 Illustration of Holimap and its advantages over the SSA. Figure taken from Jia and Grima (2024), BioRxiv published under the CC-BY-NC-ND 4.0 International licence.
First, a relatively small number of trajectories is calculated using SSA to compute the steady-state or time-dependent sample moments of protein numbers. Based on this, the effective parameters of the linear model can be approximated. Finally, the linear model can be solved using FSP and its solution mapped back as an approximate solution of the high-dimensional network. Their hybrid approach was found to be much faster than the stand-alone implementations of FSP (>1010x), Holimap (15x) and LMA (6x) at similar accuracy. When running SSA and the hybrid approach for the same CPU time, the hybrid approach performs much better in regards to the Hellinger distance, indicating the need for additional computationally expensive trajectories to achieve similar accuracy.
Abbreviations
CME: Chemical Master Equations
CPU: Central Processing Unit
FSP: Finite State Projection (Munsky & Khammash, 2006)
GRN: Gene Regulatory Network
HD: Hellinger Distance (Hellinger, 1909)
HOLIMAP: High-Order LInear-Mapping APproximation framework (Jia & Grima, 2024)
LMA: linear-mapping approximation (Cao & Grima, 2018)
LSODA: Livermore Solver for Ordinary Differential Equations with Automatic Method Switching (Petzold, 1983)
SSA: Doob-Gillespies/Stochastical Simulation Algorithm (Gillespie, 1976)
TF: Transcription Factor
Analytical Solution yield exact solutions, but they are unfeasible for complex problems
Numeric Solution yield “good enough” approximative solution
References
Cao, Z., & Grima, R. (2018). Linear mapping approximation of gene regulatory networks with stochastic dynamics. Nature communications, 9(1), 3305. https://doi.org/10.1038/s41467-018-05822-0
Dinh, K. N., & Sidje, R. B. (2016). Understanding the finite state projection and related methods for solving the chemical master equation. Physical Biology, 13(3), 035003. https://doi.org/10.1088/1478-3975/13/3/035003
Gillespie, D. T. (1976). A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. Journal of Computational Physics, 22(4), 403–434. https://doi.org/10.1016/0021-9991(76)90041-3
Hellinger, E. (1909). Neue Begründung der Theorie quadratischer Formen von unendlich vielen Veränderlichen. Journal für die reine und angewandte Mathematik, 1909(136), 210-271. https://doi.org/10.1515/crll.1909.136.210
Markov, A. A. (1953). The Theory of Algorithms. Journal of Symbolic Logic, 18(4), 340–341. https://doi.org/10.2307/2266585
Munsky, B., & Khammash, M. (2006). The finite state projection algorithm for the solution of the chemical master equation. The Journal of chemical physics, 124(4), 044104. https://doi.org/10.1063/1.2145882
Petzold, L. (1983). Automatic Selection of Methods for Solving Stiff and Nonstiff Systems of Ordinary Differential Equations. SIAM Journal on Scientific and Statistical Computing, 4(1), 136–148. https://doi.org/10.1137/0904010
doi: https://doi.org/10.1242/prelights.36895
Read preprintSign up to customise the site to your preferences and to receive alerts
Register hereAlso in the bioinformatics category:
The lipidomic architecture of the mouse brain
CRM UoE Journal Club et al.
Kosmos: An AI Scientist for Autonomous Discovery
Roberto Amadio et al.
Human single-cell atlas analysis reveals heterogeneous endothelial signaling
Charis Qi
Also in the systems biology category:
Longitudinal single cell RNA-sequencing reveals evolution of micro- and macro-states in chronic myeloid leukemia
Charis Qi
Environmental and Maternal Imprints on Infant Gut Metabolic Programming
Siddharth Singh
Single-Cell Network Analysis Identifies CLEC4E as a Key Mediator of Proinflammatory mDC Responses in Influenza Infection
Charis Qi
preLists in the bioinformatics category:
Keystone Symposium – Metabolic and Nutritional Control of Development and Cell Fate
This preList contains preprints discussed during the Metabolic and Nutritional Control of Development and Cell Fate Keystone Symposia. This conference was organized by Lydia Finley and Ralph J. DeBerardinis and held in the Wylie Center and Tupper Manor at Endicott College, Beverly, MA, United States from May 7th to 9th 2025. This meeting marked the first in-person gathering of leading researchers exploring how metabolism influences development, including processes like cell fate, tissue patterning, and organ function, through nutrient availability and metabolic regulation. By integrating modern metabolic tools with genetic and epidemiological insights across model organisms, this event highlighted key mechanisms and identified open questions to advance the emerging field of developmental metabolism.
| List by | Virginia Savy, Martin Estermann |
‘In preprints’ from Development 2022-2023
A list of the preprints featured in Development's 'In preprints' articles between 2022-2023
| List by | Alex Eve, Katherine Brown |
9th International Symposium on the Biology of Vertebrate Sex Determination
This preList contains preprints discussed during the 9th International Symposium on the Biology of Vertebrate Sex Determination. This conference was held in Kona, Hawaii from April 17th to 21st 2023.
| List by | Martin Estermann |
Alumni picks – preLights 5th Birthday
This preList contains preprints that were picked and highlighted by preLights Alumni - an initiative that was set up to mark preLights 5th birthday. More entries will follow throughout February and March 2023.
| List by | Sergio Menchero et al. |
Fibroblasts
The advances in fibroblast biology preList explores the recent discoveries and preprints of the fibroblast world. Get ready to immerse yourself with this list created for fibroblasts aficionados and lovers, and beyond. Here, my goal is to include preprints of fibroblast biology, heterogeneity, fate, extracellular matrix, behavior, topography, single-cell atlases, spatial transcriptomics, and their matrix!
| List by | Osvaldo Contreras |
Single Cell Biology 2020
A list of preprints mentioned at the Wellcome Genome Campus Single Cell Biology 2020 meeting.
| List by | Alex Eve |
Antimicrobials: Discovery, clinical use, and development of resistance
Preprints that describe the discovery of new antimicrobials and any improvements made regarding their clinical use. Includes preprints that detail the factors affecting antimicrobial selection and the development of antimicrobial resistance.
| List by | Zhang-He Goh |
Also in the systems biology category:
2024 Hypothalamus GRC
This 2024 Hypothalamus GRC (Gordon Research Conference) preList offers an overview of cutting-edge research focused on the hypothalamus, a critical brain region involved in regulating homeostasis, behavior, and neuroendocrine functions. The studies included cover a range of topics, including neural circuits, molecular mechanisms, and the role of the hypothalamus in health and disease. This collection highlights some of the latest advances in understanding hypothalamic function, with potential implications for treating disorders such as obesity, stress, and metabolic diseases.
| List by | Nathalie Krauth |
‘In preprints’ from Development 2022-2023
A list of the preprints featured in Development's 'In preprints' articles between 2022-2023
| List by | Alex Eve, Katherine Brown |
EMBL Synthetic Morphogenesis: From Gene Circuits to Tissue Architecture (2021)
A list of preprints mentioned at the #EESmorphoG virtual meeting in 2021.
| List by | Alex Eve |
Single Cell Biology 2020
A list of preprints mentioned at the Wellcome Genome Campus Single Cell Biology 2020 meeting.
| List by | Alex Eve |
ASCB EMBO Annual Meeting 2019
A collection of preprints presented at the 2019 ASCB EMBO Meeting in Washington, DC (December 7-11)
| List by | Madhuja Samaddar et al. |
EMBL Seeing is Believing – Imaging the Molecular Processes of Life
Preprints discussed at the 2019 edition of Seeing is Believing, at EMBL Heidelberg from the 9th-12th October 2019
| List by | Dey Lab |
Pattern formation during development
The aim of this preList is to integrate results about the mechanisms that govern patterning during development, from genes implicated in the processes to theoritical models of pattern formation in nature.
| List by | Alexa Sadier |








 (No Ratings Yet)
(No Ratings Yet)