Spreading of molecular mechanical perturbations on linear filaments
Posted on: 27 March 2019
Preprint posted on 11 March 2019
Making a mountain out of a molehill: interdisciplinary study by Balassy, Lauzon and Hilbert shows how local perturbations become important globally. #actin #biophysics
Selected by Lars HubatschCategories: biophysics, systems biology
How local perturbations in a system spread and influence the system as a whole is an important question in biology. Examples include trigger waves in Xenopus eggs, signal conduction in neurons and, on a much smaller scale, interactions between actin filaments or microtubules. In these examples, local interactions result in a system-wide spreading of information or mechanical coupling.
In their preprint, Balassy et al. investigate the interplay between local perturbations and system size in a well-controlled 1D geometry in an actin sliding assay. Myosins in this assay are bound to the substrate, while the motion of different length actin filaments can be observed (panels A and B). Crucially, a filament’s sliding behavior depends on its length (which corresponds to system size in their modelling). Small filaments (< 0.3 um) exhibit no sliding, intermediate sizes (< 1 mu) show a stop-and-go pattern, while longer filaments slide continuously (panels C and D).
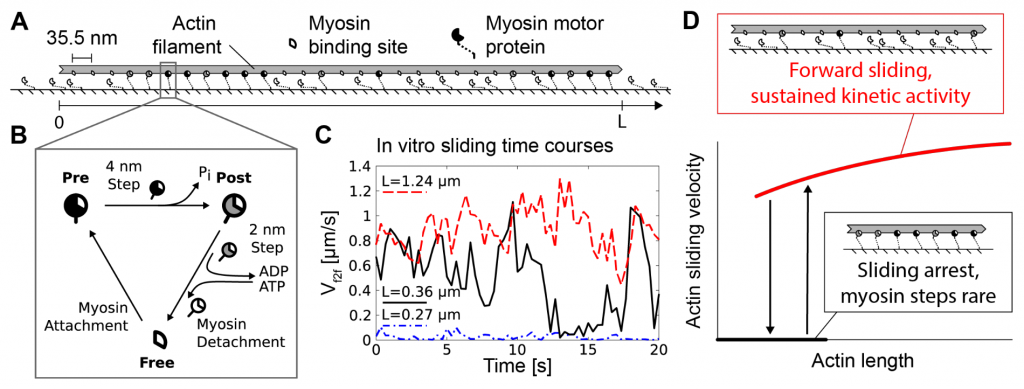
Balassy and colleagues explain this behavior within their framework for one-dimensional spreading of perturbations. Myosin arrest only becomes dominant when the arrest spreads to the length of the entire filament. This is only likely for small filaments and has less impact on intermediate and no impact on long filaments. Conversely, introducing long-term stable local arrest experimentally via filamin allows spreading of arrest to the entire filament. This impacts long filaments the most, due to the higher probability of filamin binding.
From this specific molecular picture the authors then generalize their actin-myosin theory to a more general spin chain model. The latter can in principal be mapped to many different processes, showing the generality of their findings.
Given the simplicity of the model it seems tempting to generalize at least the theory to 2D or 3D, which might introduce interesting phenomena based on a system’s geometry. For anyone in the field it is also worth looking into the specific advances of the model compared to previous attempts of modelling the same systems, however, these were too rich to cover in detail in this piece. Taken together, this is a great example of combining rigorous theory with a tractable experimental system, in order to generalize physical mechanisms.
Questions to the authors:
What other systems might this be useful in?
The emphasis lies on 1D, if the expected behavior is different in 2D, how hard would it be to generalize the theory?
Depending on the typical or useful size of a given system, interactions might need to be tuned, is this seen in vivo?
doi: https://doi.org/10.1242/prelights.9664
Read preprintSign up to customise the site to your preferences and to receive alerts
Register hereAlso in the biophysics category:
Topology changes of the regenerating Hydra define actin nematic defects as mechanical organizers of morphogenesis
Rachel Mckeown
Structural basis of respiratory complexes adaptation to cold temperatures
Pamela Ornelas
Actin polymerization drives lumen formation in a human epiblast model
Megane Rayer, Rivka Shapiro
Also in the systems biology category:
Modular control of time and space during vertebrate axis segmentation
AND
Natural genetic variation quantitatively regulates heart rate and dimension
Girish Kale, Jennifer Ann Black
Expressive modeling and fast simulation for dynamic compartments
Benjamin Dominik Maier
Clusters of lineage-specific genes are anchored by ZNF274 in repressive perinucleolar compartments
Silvia Carvalho
preLists in the biophysics category:
preLights peer support – preprints of interest
This is a preprint repository to organise the preprints and preLights covered through the 'preLights peer support' initiative.
| List by | preLights peer support |
66th Biophysical Society Annual Meeting, 2022
Preprints presented at the 66th BPS Annual Meeting, Feb 19 - 23, 2022 (The below list is not exhaustive and the preprints are listed in no particular order.)
| List by | Soni Mohapatra |
EMBL Synthetic Morphogenesis: From Gene Circuits to Tissue Architecture (2021)
A list of preprints mentioned at the #EESmorphoG virtual meeting in 2021.
| List by | Alex Eve |
Biophysical Society Meeting 2020
Some preprints presented at the Biophysical Society Meeting 2020 in San Diego, USA.
| List by | Tessa Sinnige |
ASCB EMBO Annual Meeting 2019
A collection of preprints presented at the 2019 ASCB EMBO Meeting in Washington, DC (December 7-11)
| List by | Madhuja Samaddar et al. |
EMBL Seeing is Believing – Imaging the Molecular Processes of Life
Preprints discussed at the 2019 edition of Seeing is Believing, at EMBL Heidelberg from the 9th-12th October 2019
| List by | Dey Lab |
Biomolecular NMR
Preprints related to the application and development of biomolecular NMR spectroscopy
| List by | Reid Alderson |
Biophysical Society Annual Meeting 2019
Few of the preprints that were discussed in the recent BPS annual meeting at Baltimore, USA
| List by | Joseph Jose Thottacherry |
Also in the systems biology category:
‘In preprints’ from Development 2022-2023
A list of the preprints featured in Development's 'In preprints' articles between 2022-2023
| List by | Alex Eve, Katherine Brown |
EMBL Synthetic Morphogenesis: From Gene Circuits to Tissue Architecture (2021)
A list of preprints mentioned at the #EESmorphoG virtual meeting in 2021.
| List by | Alex Eve |
Single Cell Biology 2020
A list of preprints mentioned at the Wellcome Genome Campus Single Cell Biology 2020 meeting.
| List by | Alex Eve |
ASCB EMBO Annual Meeting 2019
A collection of preprints presented at the 2019 ASCB EMBO Meeting in Washington, DC (December 7-11)
| List by | Madhuja Samaddar et al. |
EMBL Seeing is Believing – Imaging the Molecular Processes of Life
Preprints discussed at the 2019 edition of Seeing is Believing, at EMBL Heidelberg from the 9th-12th October 2019
| List by | Dey Lab |
Pattern formation during development
The aim of this preList is to integrate results about the mechanisms that govern patterning during development, from genes implicated in the processes to theoritical models of pattern formation in nature.
| List by | Alexa Sadier |









 (1 votes)
(1 votes)