Biologically informed NeuralODEs for genome-wide regulatory dynamics
Posted on: 31 May 2023 , updated on: 22 May 2024
Preprint posted on 27 February 2023
Article now published in Genome Biology at https://genomebiology.biomedcentral.com/articles/10.1186/s13059-024-03264-0
Predictive, explainable, flexible & scalable: Hossain and colleagues developed a modelling framework based on prior-informed neuralODEs (PHOENIX) to estimate gene regulatory dynamics.
Selected by Benjamin Dominik MaierCategories: bioinformatics, cancer biology, systems biology
Updated 22 May 2024 with a postLight by Benjamin Dominik Maier
Congratulations to Intekhab Hossain, Viola Fanfani, Jonas Fischer, John Quackenbush and Rebekka Burkholz! Their manuscript has been published in Genome Biology on May 21st 2024 (link to the journal article). Jonas Fischer has been added to the author list during the review process and contributed to this work with the newly added B cell modeling experiment and its interpretation.
When comparing the preprint to the published manuscript, there are two noteworthy changes:
– Firstly, the authors added a comparative quantitative analysis of PHOENIX against existing competitor methods (Dynamo, RNA-ODE, DeepVelo) as well as out-of-the-box NeuralODEs using real data (yeast and breast cancer) expanding on their previous qualitative theoretical approach (see old Table 1). The authors observed better scalability and better interpretability compared to the existing black-box models as well as a better performance compared to out-of-the-box NeuralODE models (see Table 1, Figure 6, Supp. Table 11, Supp. Table 14).
– Secondly, the authors added a case study on longitudinal RNA-seq measurements of B-cells treated with the monoclonal antibody Rituximab and an untreated control. Rituximab binds to B-cells in order to induce cell death through apoptosis, NK-mediated cytotoxicity or macrophage-mediated phagocytosis thereby acting as targeted cancer drug against B cell malignancies. Following model training, PHOENIX was found to accurately model the gene expression dynamics of both conditions. When looking at changes in regulatory dynamics, the authors identified several key regulators of apoptosis (see Supp. Figures S11 & S12 as well as Supp. Table S15) highlighting the biological interpretability of the results.
For more details and reasoning on modifications of the manuscript, please have a look at the published reviewer correspondence which can be found here.
Background:
Modelling Gene Regulatory Networks (GRNs)
A gene regulatory network (GRN) is a conceptual model that explains how genes and their regulatory elements (e.g. transcription factors) interact within a cell (Karlebach & Shamir, 2008). These directional interactions between genes and their products can be modelled as a system of coupled ordinary differential equations (ODEs) with activations or repressions represented as positive or negative terms. As the ODE model describes how the concentrations of each component change over time, it can help to causally explain temporal gene expression patterns.
ODE models are constructed based on existing knowledge of the network structure and kinetic parameters, which can be derived from literature or experimental data. Unknown parameters can be iteratively estimated by minimising the difference between predicted values and the true values of the training dataset. The function that is used to compute this difference/error is called loss function or cost function. After validating the model with independent data, ODE models can predict and study GRN behaviour under various conditions, such as environmental changes or gene mutations. The model can therefore be solved numerically using inter alia the Runge-Kutta or Euler’s methods (for visualisations check out the blog entry by Harold Serrano) to simulate GRN dynamics (Griffiths & Higham, 2010). In short, the Runge-Kutta method estimates the value of y for a given x by computing slopes at individual points and taking the weighted averages of them thereby approximating first-order ordinary differential equations.
Neural Ordinary Differential Equations (NeuralODE)
Neural Ordinary Differential Equations are a type of neural network architecture that directly model the continuous evolution of a system using ordinary differential equations (Chen et al., 2018). The input to the model is a set of initial conditions and an ODE-based function that describes the change in the system over time as a continuous trajectory. The neural network is then trained to learn the parameters of the ODE function that best fit the training data. Neural ODEs have shown promising results in a variety of applications, including image classification (Paoletti et al., 2020), time-series prediction (Jin et al., 2022), and physical simulations (Lanzieri et al., 2022; Kong et al., 2022; Lai et al., 2022).
For readers interested in the topic, I can warmly recommend to read the more detailed introduction to (neural) ODEs by Jonty Sinai, which can be found at https://jontysinai.github.io/jekyll/update/2019/01/18/understanding-neural-odes.html. An overview of different ML methods to infer gene regulatory networks can be found in Table 1 of the featured preprint.

Fig. 1 PHOENIX Neural ODE framework. Figure taken from Hossain et al. (2023), BioRxiv published under the CC-BY-NC-ND 4.0 International license.
Out-of-the-box models (OOTB models)
Out-of-the-box or pre-trained NLP models are machine learning models that are trained on general purpose data sources. Even though they tend not to be tailored to specific questions/applications, they are popular for pioneering and benchmarking routines as they can be used immediately without time-/resource-expensive customization or training on specific datasets.
Key Findings
The authors developed their ML-framework PHOENIX (Prior-informed Hill-like ODEs to Enhance Neuralnet Integrals with eXplainability) to overcome pitfalls of previously published methods and obtain biologically more meaningful results (GitHub). To better represent the non-linear activation or inhibition of biological processes, the authors incorporated sigmoid Hill-Langmuir-like kinetics (Frank, 2013), which are commonly used when modelling pharmacological reactions, signal transduction and gene expression processes. The Hill-Langmuir equation accounts for saturation effects and cooperative processes such as transcription factors being able to bind to DNA molecules via multiple binding sites thereby increasing the gene expression rate (Chu et al., 2009). Moreover, Hill-like kinetics have been shown to better resemble noise filter-induced bimodality (Ochab-Marcinek et al., 2017), which cannot be resolved using linear dynamics.
Secondly, the PHOENIX ML-framework allows users to integrate prior domain knowledge models to leverage prior expert domain knowledge and create explainable model representations in sparse and noisy settings.
Dynamics from noisy simulated GRN
Hossain and colleagues tested PHOENIX on simulated gene expression data from two in silico systems using 150 trajectories (140 training / 10 testing) with varying noise levels. When compared to the ground truth (i.e. the original non-noisy data), PHOENIX was found to perform better than out-of-the-box models and previously published methods across different noise levels. PHOENIX successfully recovered the true, i.e. unnoisy gene expression patterns over time despite very noisy training trajectories and prior knowledge models. While prior-less PHOENIX demonstrated the highest predictability overall, adding a user-supplied prior knowledge model resulted in a better explainability.
Recovery of sparse causal biology
Next, the authors quantified the effect of misspecified prior knowledge models on the PHOENIX prediction to assess whether the model can learn causal elements in the system beyond the ones given in the prior knowledge model. They determined that PHOENIX is able to infer regulatory interactions from just the data itself and – if needed – can also deviate from the prior knowledge.
Oscillating yeast cell cycle dynamics
To assess how their framework performs on real biological data, the authors applied PHOENIX to time-resolved expression values of synchronised yeast cells during the cell cycle. Even though the authors had two experimental replicates, they decided against using one for training and one for validation as the high similarity between the replicates would have yielded artificially good results. Hence the data was split into transition pairs, i.e. always taking expression vectors from two consecutive time points with a 86%/7%/7% split (training, validation, testing). When comparing the prediction results to ChIP-chip transcription factor (TF) binding data, it seemed like the model had not only learned to explain temporal patterns in expression, but could also accurately predict TF binding. Moreover, the model predicted the continued periodic oscillations of the cell cycle, even though there were only two cycles present in the data and the ML framework was based on Hill-like kinetics. Hence, this result demonstrates that while predicting the dynamics accurately, the model is flexible enough to deviate from its kinetic framework and the prior knowledge model.
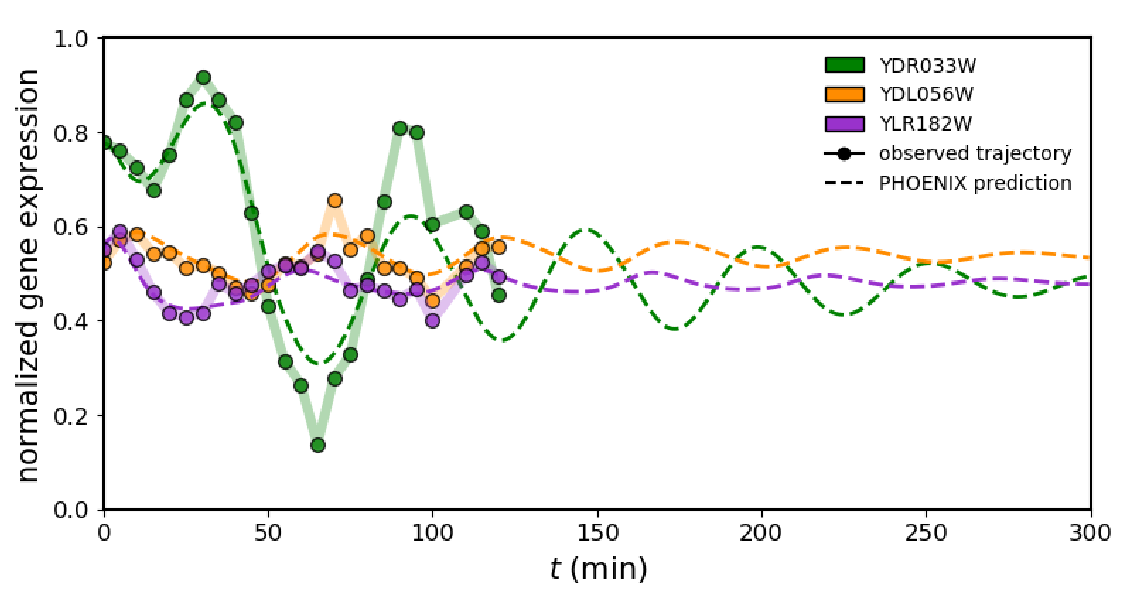
Fig. 2 PHOENIX prediction of yeast cell-cycle dynamics. Figure taken from Hossain et al. (2023), BioRxiv published under the CC-BY-NC-ND 4.0 International license.
Large-scale breast cancer dynamcis
Most computational approaches to infer gene regulatory networks are not scalable to human-genome scale networks (> 25,000 genes). To assess whether PHOENIX is extendable to large-scale human expression data, publicly available microarray expression values for 22,000 genes from 198 breast cancer patients were obtained and ordered in pseudotime. After excluding genes with no measurable expression, the data was split 90%/5%/5% into training, validation and testing data. PHOENIX predictions were found to be in agreement with a validation network of experimental ChIP-chip binding information, even when including all genes with measurable expression. Next, they perturbed the initial expression of each gene in silico and studied the effect on the predicted expressions of all other genes. Perturbations of (cancer-relevant) transcription factor genes and known cancer drivers were found to have the largest effects on overall gene expression, which is in line with prior literature knowledge. To test whether the full gene set is required for obtaining biological interpretable results, the authors reduced the number of included genes considerably. This resulted in a loss of mechanistic explainability of the resulting regulatory model as well as failing to identify previously found cancer-relevant pathways in a pathway-based functional enrichment analysis. Therefore, the authors concluded that there is a need and benefit for genome-scale predictors and that reducing the complexity of a predictor comes at the cost of explainability.
Conclusion and Perspective
While ODE’s have a long history in applied and pure mathematics, it is fascinating to see the transition to high-dimensional machine-learning algorithms with millions of parameters solving applied mathematical problems. Neural ODEs slowly close the gap between traditional mechanism-driven mathematical modelling and more data-driven ML-approaches. Given the enormous flexibility of neural networks as well as the development of even more sophisticated and highly optimised computing frameworks, it will be interesting to see which applied mathematical problems we might be able to solve in the next decade. Still, traditional approaches will remain indispensable for biological mathematical modelling.
I decided to feature this preprint from Intekhab Hossain and colleagues after his fantastic talk (link to recording) and poster presentation at the 15th RECOMB Satellite Workshop on Computational Cancer Biology in Istanbul earlier this year. Besides it being potentially very useful for my current PhD project, PHOENIX stood out to me as it allows the flexible integration of prior expert knowledge and is data-driven while at the same still mechanism-driven. Taken together, the ML-framework seems to be quite easily adaptable for a wide range of applications. Even though many researchers are pushing for interpretable models, a lot of researchers try to explain their black box models rather than developing explainable models from the beginning (see Rudin, 2019). Hence, I really like the approach chosen by Intekhab Hossain and colleagues.
Further Material
Tags/Keywords
Ordinary Differential Equation (ODE), Gene-Regulatory Network (GRN), Neural Network, Mathematical Modelling, Machine Learning
References
Chen, R. T. Q., Rubanova, Y., Bettencourt, J., & Duvenaud, D. (2018). Neural Ordinary Differential Equations (Version 5). arXiv. https://doi.org/10.48550/ARXIV.1806.07366
Chu, D., Zabet, N. R., & Mitavskiy, B. (2009). Models of transcription factor binding: Sensitivity of activation functions to model assumptions. Journal of Theoretical Biology (Vol. 257, Issue 3, pp. 419–429). https://doi.org/10.1016/j.jtbi.2008.11.026
Frank, S. A. (2013). Input-output relations in biological systems: measurement, information and the Hill equation. Biology Direct (Vol. 8, Issue 1). https://doi.org/10.1186/1745-6150-8-31
Griffiths, D. F., & Higham, D. J. (2010). Numerical methods for ordinary differential equations (2010th ed.). Guildford, England: Springer.
Jin, M., Zheng, Y., Li, Y.-F., Chen, S., Yang, B., & Pan, S. (2022). Multivariate Time Series Forecasting with Dynamic Graph Neural ODEs. IEEE Transactions on Knowledge and Data Engineering (pp. 1–14). Institute of Electrical and Electronics Engineers (IEEE). https://doi.org/10.1109/tkde.2022.3221989
Karlebach, G., Shamir, R. (2008) Modelling and analysis of gene regulatory networks. Nat Rev Mol Cell Biol 9, 770–780. https://doi.org/10.1038/nrm2503
Kong, X., Yamashita, K., Foggo, B., & Yu, N. (2022). Dynamic Parameter Estimation with Physics-based Neural Ordinary Differential Equations. 2022 IEEE Power & Energy Society General Meeting (PESGM). https://doi.org/10.1109/pesgm48719.2022.9916840
Lai, Z., Liu, W., Jian, X., Bacsa, K., Sun, L., & Chatzi, E. (2022). Neural modal ordinary differential equations: Integrating physics-based modeling with neural ordinary differential equations for modeling high-dimensional monitored structures. Data-Centric Engineering, 3, E34. https://doi.org/10.1017/dce.2022.35
Lanzieri, D., Lanusse, F., & Starck, J.-L. (2022). Hybrid Physical-Neural ODEs for Fast N-body Simulations (Version 2). arXiv. https://doi.org/10.48550/ARXIV.2207.05509
Ochab-Marcinek, A., Jędrak, J., & Tabaka, M. (2017). Hill kinetics as a noise filter: the role of transcription factor autoregulation in gene cascades. Physical Chemistry Chemical Physics (Vol. 19, Issue 33, pp. 22580–22591).https://doi.org/10.1039/c7cp00743d
Paoletti, M. E., Haut, J. M., Plaza, J., & Plaza, A. (2020). Neural Ordinary Differential Equations for Hyperspectral Image Classification. IEEE Transactions on Geoscience and Remote Sensing (Vol. 58, Issue 3, pp. 1718–1734). Institute of Electrical and Electronics Engineers (IEEE). https://doi.org/10.1109/tgrs.2019.2948031
Rudin, C. (2019) Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat Mach Intell 1, 206–215. https://doi.org/10.1038/s42256-019-0048-x
doi: https://doi.org/10.1242/prelights.34751
Read preprintHave your say
Sign up to customise the site to your preferences and to receive alerts
Register hereAlso in the bioinformatics category:
The lipidomic architecture of the mouse brain
CRM UoE Journal Club et al.
Kosmos: An AI Scientist for Autonomous Discovery
Roberto Amadio et al.
Human single-cell atlas analysis reveals heterogeneous endothelial signaling
Charis Qi
Also in the cancer biology category:
A Novel Chimeric Antigen Receptor (CAR) - Strategy to Target EGFRVIII-Mutated Glioblastoma Cells via Macrophages
Dina Kabbara
Taxane-Induced Conformational Changes in the Microtubule Lattice Activate GEF-H1-Dependent RhoA Signaling
Vibha SINGH
ROCK2 inhibition has a dual role in reducing ECM remodelling and cell growth, while impairing migration and invasion
Sharvari Pitke
Also in the systems biology category:
Human single-cell atlas analysis reveals heterogeneous endothelial signaling
Charis Qi
Longitudinal single cell RNA-sequencing reveals evolution of micro- and macro-states in chronic myeloid leukemia
Charis Qi
Environmental and Maternal Imprints on Infant Gut Metabolic Programming
Siddharth Singh
preLists in the bioinformatics category:
Keystone Symposium – Metabolic and Nutritional Control of Development and Cell Fate
This preList contains preprints discussed during the Metabolic and Nutritional Control of Development and Cell Fate Keystone Symposia. This conference was organized by Lydia Finley and Ralph J. DeBerardinis and held in the Wylie Center and Tupper Manor at Endicott College, Beverly, MA, United States from May 7th to 9th 2025. This meeting marked the first in-person gathering of leading researchers exploring how metabolism influences development, including processes like cell fate, tissue patterning, and organ function, through nutrient availability and metabolic regulation. By integrating modern metabolic tools with genetic and epidemiological insights across model organisms, this event highlighted key mechanisms and identified open questions to advance the emerging field of developmental metabolism.
| List by | Virginia Savy, Martin Estermann |
‘In preprints’ from Development 2022-2023
A list of the preprints featured in Development's 'In preprints' articles between 2022-2023
| List by | Alex Eve, Katherine Brown |
9th International Symposium on the Biology of Vertebrate Sex Determination
This preList contains preprints discussed during the 9th International Symposium on the Biology of Vertebrate Sex Determination. This conference was held in Kona, Hawaii from April 17th to 21st 2023.
| List by | Martin Estermann |
Alumni picks – preLights 5th Birthday
This preList contains preprints that were picked and highlighted by preLights Alumni - an initiative that was set up to mark preLights 5th birthday. More entries will follow throughout February and March 2023.
| List by | Sergio Menchero et al. |
Fibroblasts
The advances in fibroblast biology preList explores the recent discoveries and preprints of the fibroblast world. Get ready to immerse yourself with this list created for fibroblasts aficionados and lovers, and beyond. Here, my goal is to include preprints of fibroblast biology, heterogeneity, fate, extracellular matrix, behavior, topography, single-cell atlases, spatial transcriptomics, and their matrix!
| List by | Osvaldo Contreras |
Single Cell Biology 2020
A list of preprints mentioned at the Wellcome Genome Campus Single Cell Biology 2020 meeting.
| List by | Alex Eve |
Antimicrobials: Discovery, clinical use, and development of resistance
Preprints that describe the discovery of new antimicrobials and any improvements made regarding their clinical use. Includes preprints that detail the factors affecting antimicrobial selection and the development of antimicrobial resistance.
| List by | Zhang-He Goh |
Also in the cancer biology category:
October in preprints – Cell biology edition
Different preLighters, with expertise across cell biology, have worked together to create this preprint reading list for researchers with an interest in cell biology. This month, most picks fall under (1) Cell organelles and organisation, followed by (2) Mechanosignaling and mechanotransduction, (3) Cell cycle and division and (4) Cell migration
| List by | Matthew Davies et al. |
September in preprints – Cell biology edition
A group of preLighters, with expertise in different areas of cell biology, have worked together to create this preprint reading list. This month, categories include: (1) Cell organelles and organisation, (2) Cell signalling and mechanosensing, (3) Cell metabolism, (4) Cell cycle and division, (5) Cell migration
| List by | Sristilekha Nath et al. |
July in preprints – the CellBio edition
A group of preLighters, with expertise in different areas of cell biology, have worked together to create this preprint reading lists for researchers with an interest in cell biology. This month, categories include: (1) Cell Signalling and Mechanosensing (2) Cell Cycle and Division (3) Cell Migration and Cytoskeleton (4) Cancer Biology (5) Cell Organelles and Organisation
| List by | Girish Kale et al. |
June in preprints – the CellBio edition
A group of preLighters, with expertise in different areas of cell biology, have worked together to create this preprint reading lists for researchers with an interest in cell biology. This month, categories include: (1) Cell organelles and organisation (2) Cell signaling and mechanosensation (3) Genetics/gene expression (4) Biochemistry (5) Cytoskeleton
| List by | Barbora Knotkova et al. |
May in preprints – the CellBio edition
A group of preLighters, with expertise in different areas of cell biology, have worked together to create this preprint reading lists for researchers with an interest in cell biology. This month, categories include: 1) Biochemistry/metabolism 2) Cancer cell Biology 3) Cell adhesion, migration and cytoskeleton 4) Cell organelles and organisation 5) Cell signalling and 6) Genetics
| List by | Barbora Knotkova et al. |
Keystone Symposium – Metabolic and Nutritional Control of Development and Cell Fate
This preList contains preprints discussed during the Metabolic and Nutritional Control of Development and Cell Fate Keystone Symposia. This conference was organized by Lydia Finley and Ralph J. DeBerardinis and held in the Wylie Center and Tupper Manor at Endicott College, Beverly, MA, United States from May 7th to 9th 2025. This meeting marked the first in-person gathering of leading researchers exploring how metabolism influences development, including processes like cell fate, tissue patterning, and organ function, through nutrient availability and metabolic regulation. By integrating modern metabolic tools with genetic and epidemiological insights across model organisms, this event highlighted key mechanisms and identified open questions to advance the emerging field of developmental metabolism.
| List by | Virginia Savy, Martin Estermann |
April in preprints – the CellBio edition
A group of preLighters, with expertise in different areas of cell biology, have worked together to create this preprint reading lists for researchers with an interest in cell biology. This month, categories include: 1) biochemistry/metabolism 2) cell cycle and division 3) cell organelles and organisation 4) cell signalling and mechanosensing 5) (epi)genetics
| List by | Vibha SINGH et al. |
March in preprints – the CellBio edition
A group of preLighters, with expertise in different areas of cell biology, have worked together to create this preprint reading lists for researchers with an interest in cell biology. This month, categories include: 1) cancer biology 2) cell migration 3) cell organelles and organisation 4) cell signalling and mechanosensing 5) genetics and genomics 6) other
| List by | Girish Kale et al. |
Biologists @ 100 conference preList
This preList aims to capture all preprints being discussed at the Biologists @100 conference in Liverpool, UK, either as part of the poster sessions or the (flash/short/full-length) talks.
| List by | Reinier Prosee, Jonathan Townson |
February in preprints – the CellBio edition
A group of preLighters, with expertise in different areas of cell biology, have worked together to create this preprint reading lists for researchers with an interest in cell biology. This month, categories include: 1) biochemistry and cell metabolism 2) cell organelles and organisation 3) cell signalling, migration and mechanosensing
| List by | Barbora Knotkova et al. |
BSCB-Biochemical Society 2024 Cell Migration meeting
This preList features preprints that were discussed and presented during the BSCB-Biochemical Society 2024 Cell Migration meeting in Birmingham, UK in April 2024. Kindly put together by Sara Morais da Silva, Reviews Editor at Journal of Cell Science.
| List by | Reinier Prosee |
CSHL 87th Symposium: Stem Cells
Preprints mentioned by speakers at the #CSHLsymp23
| List by | Alex Eve |
Journal of Cell Science meeting ‘Imaging Cell Dynamics’
This preList highlights the preprints discussed at the JCS meeting 'Imaging Cell Dynamics'. The meeting was held from 14 - 17 May 2023 in Lisbon, Portugal and was organised by Erika Holzbaur, Jennifer Lippincott-Schwartz, Rob Parton and Michael Way.
| List by | Helen Zenner |
CellBio 2022 – An ASCB/EMBO Meeting
This preLists features preprints that were discussed and presented during the CellBio 2022 meeting in Washington, DC in December 2022.
| List by | Nadja Hümpfer et al. |
Fibroblasts
The advances in fibroblast biology preList explores the recent discoveries and preprints of the fibroblast world. Get ready to immerse yourself with this list created for fibroblasts aficionados and lovers, and beyond. Here, my goal is to include preprints of fibroblast biology, heterogeneity, fate, extracellular matrix, behavior, topography, single-cell atlases, spatial transcriptomics, and their matrix!
| List by | Osvaldo Contreras |
Single Cell Biology 2020
A list of preprints mentioned at the Wellcome Genome Campus Single Cell Biology 2020 meeting.
| List by | Alex Eve |
ASCB EMBO Annual Meeting 2019
A collection of preprints presented at the 2019 ASCB EMBO Meeting in Washington, DC (December 7-11)
| List by | Madhuja Samaddar et al. |
Lung Disease and Regeneration
This preprint list compiles highlights from the field of lung biology.
| List by | Rob Hynds |
Anticancer agents: Discovery and clinical use
Preprints that describe the discovery of anticancer agents and their clinical use. Includes both small molecules and macromolecules like biologics.
| List by | Zhang-He Goh |
Biophysical Society Annual Meeting 2019
Few of the preprints that were discussed in the recent BPS annual meeting at Baltimore, USA
| List by | Joseph Jose Thottacherry |
Also in the systems biology category:
2024 Hypothalamus GRC
This 2024 Hypothalamus GRC (Gordon Research Conference) preList offers an overview of cutting-edge research focused on the hypothalamus, a critical brain region involved in regulating homeostasis, behavior, and neuroendocrine functions. The studies included cover a range of topics, including neural circuits, molecular mechanisms, and the role of the hypothalamus in health and disease. This collection highlights some of the latest advances in understanding hypothalamic function, with potential implications for treating disorders such as obesity, stress, and metabolic diseases.
| List by | Nathalie Krauth |
‘In preprints’ from Development 2022-2023
A list of the preprints featured in Development's 'In preprints' articles between 2022-2023
| List by | Alex Eve, Katherine Brown |
EMBL Synthetic Morphogenesis: From Gene Circuits to Tissue Architecture (2021)
A list of preprints mentioned at the #EESmorphoG virtual meeting in 2021.
| List by | Alex Eve |
Single Cell Biology 2020
A list of preprints mentioned at the Wellcome Genome Campus Single Cell Biology 2020 meeting.
| List by | Alex Eve |
ASCB EMBO Annual Meeting 2019
A collection of preprints presented at the 2019 ASCB EMBO Meeting in Washington, DC (December 7-11)
| List by | Madhuja Samaddar et al. |
EMBL Seeing is Believing – Imaging the Molecular Processes of Life
Preprints discussed at the 2019 edition of Seeing is Believing, at EMBL Heidelberg from the 9th-12th October 2019
| List by | Dey Lab |
Pattern formation during development
The aim of this preList is to integrate results about the mechanisms that govern patterning during development, from genes implicated in the processes to theoritical models of pattern formation in nature.
| List by | Alexa Sadier |








 (No Ratings Yet)
(No Ratings Yet)
3 years
Benjamin Dominik Maier
Intekhab Hossain (ihossain@g.harvard.edu), the first author of this study, is happy to answer questions and guide users through the setup process of PHOENIX, so feel free to send him a message or comment here 🙂