Periodic spatial patterning with a single morphogen
Posted on: 24 May 2022 , updated on: 9 June 2022
Preprint posted on 22 March 2022
Article now published in Cell Systems at http://dx.doi.org/10.1016/j.cels.2022.11.001
Synthesising a zebra’s stripes: modelling a novel minimal genetic circuit for periodic patterning
Selected by Jake Cornwall-ScoonesCategories: developmental biology
Background
How tissues establish and maintain spatial organisation remains a guiding question in studies of development, homeostasis and regeneration. Spatial organisation of cell types — pattern formation — is critical for tissue functionality. Hence, deciphering the mechanisms that establish this order helps to trace causes of organ dysregulation, and to refine tissue engineering strategies.
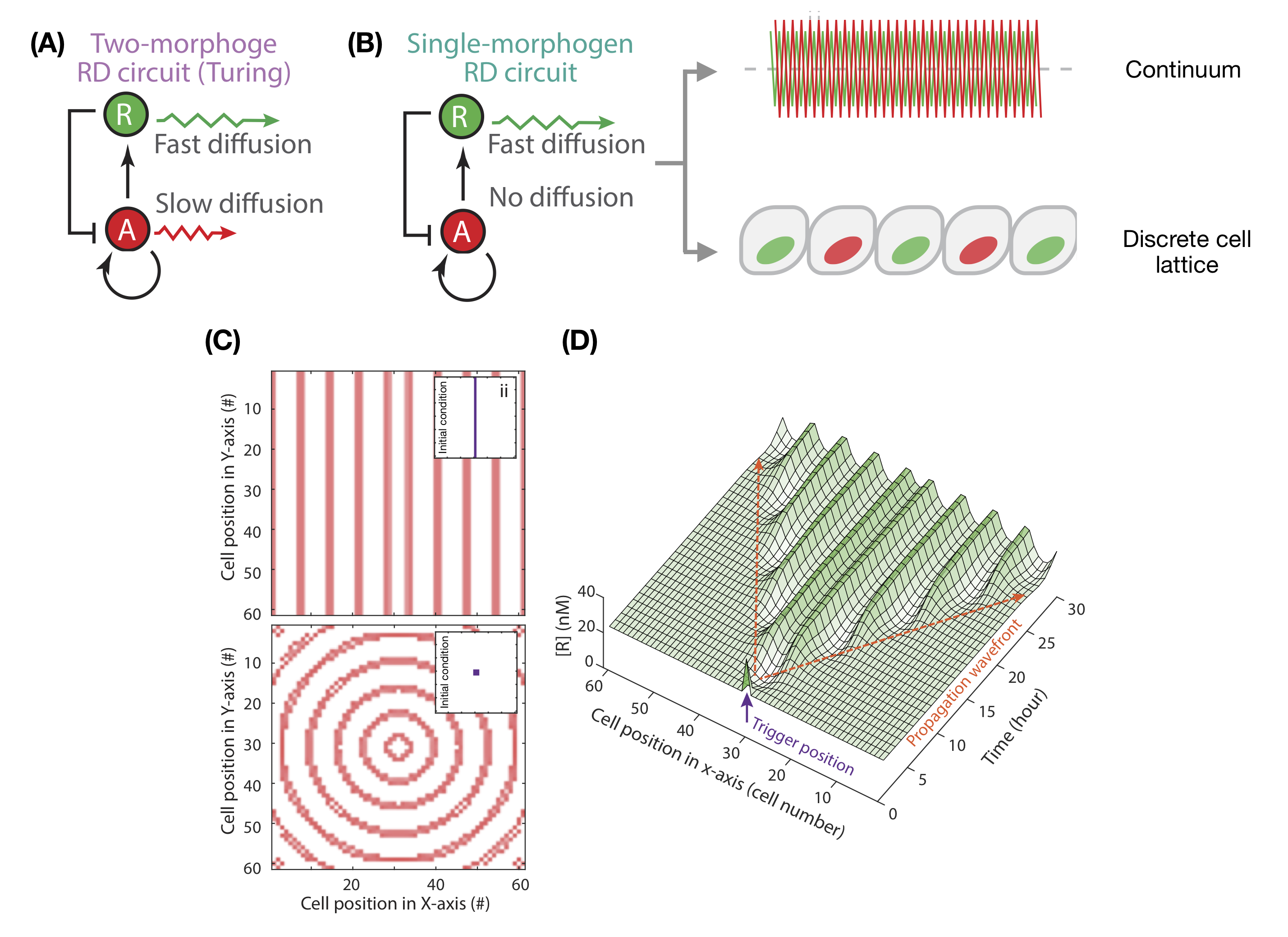
Seventy years ago, Alan Turing proposed a two-morphogen circuit to explain periodic patterning [1]. A slow-diffusing activator morphogen promotes the expression of itself as well as of a fast- diffusing repressor morphogen (Fig. 1a). This in turn represses the activator. Activator-inhibitor circuits, or generic mechanisms of local-activation and long-range inhibition[2, 3] , can facilitate spontaneous symmetry breaking in homogeneous tissues. These models have been successful in explaining the development of hair follicles [4], feather buds [5] and mammalian palate rugae [6].
Traditional Turing mechanisms involve a stringent constraint on morphogen diffusibility: one morphogen must diffuse faster than the other. This presents a challenge for validating putative examples of natural Turing patterning, given measuring morphogen diffusion is notoriously challenging [7], and for building synthetic patterning circuits. Recent theoretical work has shown that these constraints can be relaxed when additional non-diffusible species are included in the circuit [8], shown experimentally for digit patterning [9].
In this pre-print, Wang et al. demonstrate that periodic patterning can be achieved by simpler mechanisms than previously anticipated, providing new perspectives on natural patterning and scope for synthetic patterning circuit design.
Key findings
A single morphogen can generate spatial patterns.
In classical Turing systems, spatial separation between patterned domains is associated with the speed of morphogen diffusion. When activator diffusion approaches zero, spacing becomes negligible. In contrast to the idealised continuum model, biological space is discretised by cell-boundaries, placing a hard-limit on patterning length-scale. Exploring patterning on a discretised cell lattice for an extreme case where activators cannot diffuse beyond cellular boundaries, Wang et al. demonstrate through simulations that tissues can nonetheless break symmetry. Such cases are however limited in patterning length-scale, at most establishing expression patterns that repeat every cell pair (Fig. 1b).
The authors then diverge from a standard analysis of Turing systems, which generally investigate symmetry breaking from the homogeneous steady-state, instead analysing patterning dynamics when tissues are initialised with a small domain of heightened activator expression. Remarkably, these simulations establish periodic patterns of activator expression, laid down sequentially behind a propagation wavefront (Fig. 1c-d). The simple single-morphogen circuit is capable of sequentially replicating the initial perturbation at equal spacings, generating concentric rings of activation when initialised with a spot, or repeated stripes when initialised with a line. In natural development, this initial perturbation could be provided by an initial pre-pattern or a boundary cue.
Noise can abbrogate patterning capacity.
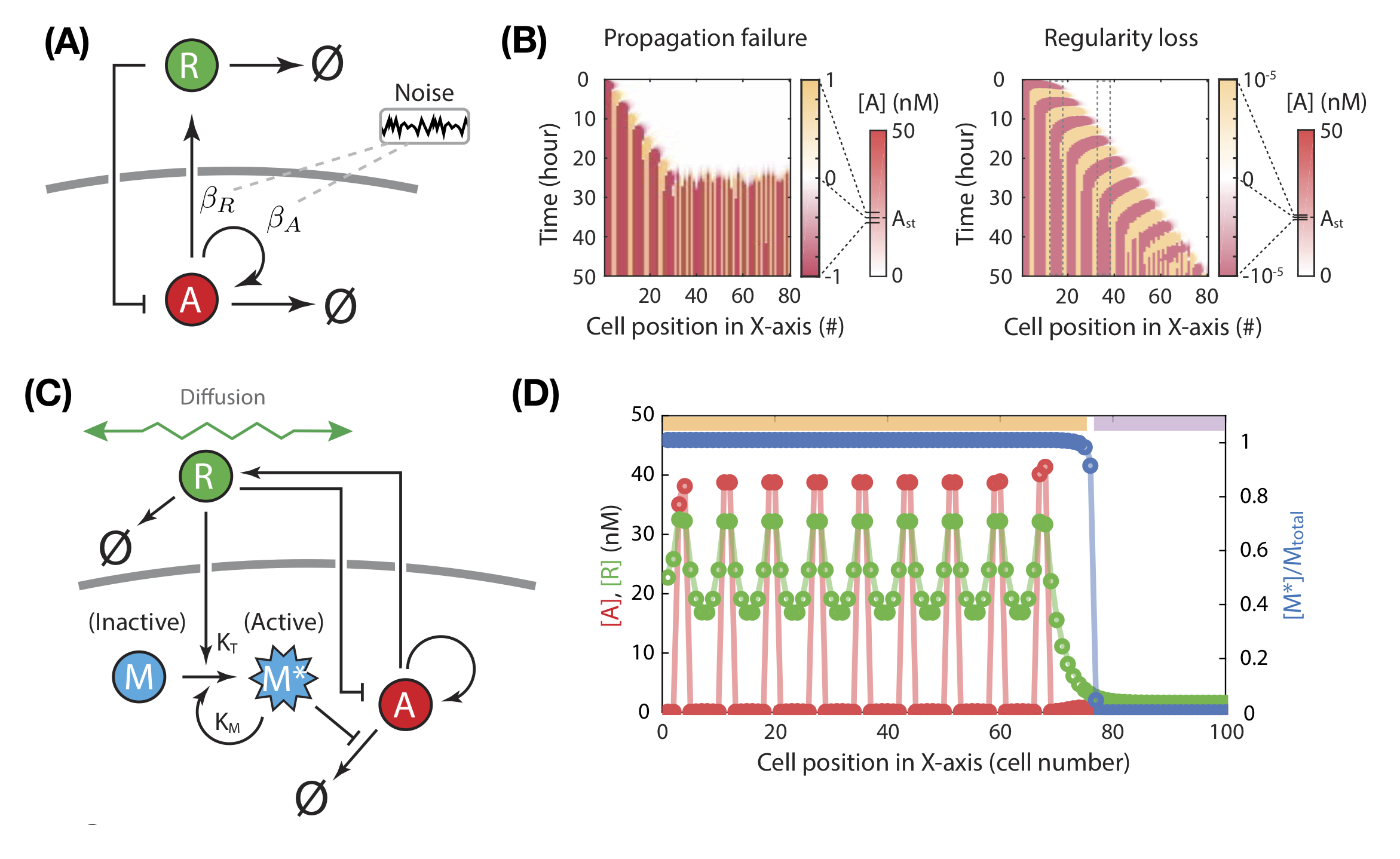
To establish patterns robustly, both natural and synthetic development need to cope with fluctuations. Noise (e.g. transcriptional bursting) presents an unavoidable constraint. The authors show that patterning is disrupted with even small noise amplitudes under this model, as measured by a failure to propagate further iterations, and regularity loss in the resultant pattern (Fig. 2a-b). Noise acutely affects unpatterned regions: existing domains of activator-expression are maintained despite higher noise levels. Thus, depending on the spatiotemporal context, the feedback architecture of the circuit can either favour or disfavour patterning robustness: strong feedback between the activator and repressor sustains patterned domains against noise, yet the same feedback amplifies random fluctuations in unpatterned regions.
Strategies for robust patterning
These analyses inspired the authors to elaborate the circuit, optimising feedback strength to maintain existing patterns while minimising noise-induced spurious initiation. They added a modulator species that is activated by the repressor i.e. only in the vicinity of the patterned domain (Fig. 2c). The active modulator inhibits activator degradation. This wiring therefore establishes two regimes: in the presence of active modulator, the circuit is primed for patterning, allowing new iterations to emerge nearby existing patterns. In its absence, patterning is muted. Simulations confirm that this novel circuit is more robust to noise than the original two-component model (Fig. 2d).
Instead of a spatial window of patterning competency, tissues may alternatively use dynamic boundaries to buffer noise. Wang et al. consider a simple model of tissue expansion: boundary cells progressively divide, providing new cells to participate in patterning. Coupling growth and patterning provides a strategy to buffer against noise, provided growth and patterning occur at similar speeds. Given periodic patterning often occurs in tandem with tissue growth (e.g. somites [10], digit phalanges [11]), evolution may have used this property as a design strategy.
What I liked about this pre-print
While Turing mechanisms have been posited to explain patterning across many developmental processes, connecting abstracted theory to cellular processes remains an active area of research. This work provides an important step to connect theory and biology, analysing plausible genetic circuits, and considering how natural constraints on spatial order — cell boundaries — can facilitate periodic patterning. The emphasis of translating the theoretical findings into testable biological hypotheses is compelling, providing blueprints for engineerable synthetic circuits and exploring patterning robustness in the face of noise. More generally, the work contributes to a growing literature that is redefining how we view morphogens, beyond the dichotomy between positional information and reaction-diffusion [12].
References
[1] Turing, A. (1952). The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 237(641), 37-72.
[2] Koch, A. J., & Meinhardt, H. (1994). Biological pattern formation: from basic mechanisms to complex structures. Reviews of modern physics, 66(4), 1481.
[3] Kondo, S., & Miura, T. (2010). Reaction-diffusion model as a framework for understanding biological pattern formation. Science, 329(5999), 1616-1620.
[4] Sick, S., Reinker, S., Timmer, J. and Schlake, T., (2006). WNT and DKK determine hair follicle spacing through a reaction-diffusion mechanism. Science, 314(5804), 1447-1450.
[5] Ho, W.K., Freem, L., Zhao, D., Painter, K.J., Woolley, T.E., Gaffney, E.A., McGrew, M.J., Tzika, A., Milinkovitch, M.C., Schneider, P. and Drusko, A., (2019). Feather arrays are patterned by interacting signalling and cell density waves. PLoS biology, 17(2), e3000132.
[6] Economou, A.D., Ohazama, A., Porntaveetus, T., Sharpe, P.T., Kondo, S., Basson, M.A., Gritli-Linde, A., Cobourne, M.T. and Green, J., (2012). Periodic stripe formation by a Turing mechanism operating at growth zones in the mammalian palate. Nature genetics, 44(3), 348-351.
[7] Müller, P., Rogers, K.W., Yu, S.R., Brand, M. and Schier, A.F., (2013). Morphogen transport. Development, 140(8), 1621-1638.
[8] Marcon, L., Diego, X., Sharpe, J. and Müller, P., (2016). High-throughput mathematical analysis identifies Turing networks for patterning with equally diffusing signals. Elife, 5, e14022.
[9] Raspopovic, J., Marcon, L., Russo, L., & Sharpe, J. (2014). Digit patterning is controlled by a Bmp-Sox9-Wnt Turing network modulated by morphogen gradients. Science, 345(6196), 566-570.
[10] Soroldoni, D., Jörg, D.J., Morelli, L.G., Richmond, D.L., Schindelin, J., Jülicher, F. and Oates, A.C., (2014). A Doppler effect in embryonic pattern formation. Science, 345(6193), 222-225.
[11] Huang, B. L., Trofka, A., Furusawa, A., Norrie, J. L., Rabinowitz, A. H., Vokes, S. A., … & Mackem, S. (2016). An interdigit signalling centre instructs coordinate phalanx-joint formation governed by 5′ Hoxd–Gli3 antagonism. Nature communications, 7(1), 1-10.
[12] Green, J.B. and Sharpe, J., 2015. Positional information and reaction-diffusion: two big ideas in developmental biology combine. Development, 142(7), pp.1203-1211.
[13] Werner, S., Stückemann, T., Amigo, M. B., Rink, J. C., Jülicher, F., & Friedrich, B. M. (2015). Scaling and regeneration of self-organized patterns. Physical review letters, 114(13), 138101.
[14] Jörg, D. J., Kitadate, Y., Yoshida, S., & Simons, B. D. (2019). Competition for stem cell fate determinants as a mechanism for tissue homeostasis. arXiv preprint arXiv:1901.03903.
doi: https://doi.org/10.1242/prelights.32174
Read preprintSign up to customise the site to your preferences and to receive alerts
Register hereAlso in the developmental biology category:
Gestational exposure to high heat-humidity conditions impairs mouse embryonic development
Girish Kale, preLights peer support
Modular control of time and space during vertebrate axis segmentation
AND
Natural genetic variation quantitatively regulates heart rate and dimension
Girish Kale, Jennifer Ann Black
Notch3 is a genetic modifier of NODAL signalling for patterning asymmetry during mouse heart looping
Bhaval Parmar
preLists in the developmental biology category:
BSDB/GenSoc Spring Meeting 2024
A list of preprints highlighted at the British Society for Developmental Biology and Genetics Society joint Spring meeting 2024 at Warwick, UK.
| List by | Joyce Yu, Katherine Brown |
GfE/ DSDB meeting 2024
This preList highlights the preprints discussed at the 2024 joint German and Dutch developmental biology societies meeting that took place in March 2024 in Osnabrück, Germany.
| List by | Joyce Yu |
‘In preprints’ from Development 2022-2023
A list of the preprints featured in Development's 'In preprints' articles between 2022-2023
| List by | Alex Eve, Katherine Brown |
preLights peer support – preprints of interest
This is a preprint repository to organise the preprints and preLights covered through the 'preLights peer support' initiative.
| List by | preLights peer support |
The Society for Developmental Biology 82nd Annual Meeting
This preList is made up of the preprints discussed during the Society for Developmental Biology 82nd Annual Meeting that took place in Chicago in July 2023.
| List by | Joyce Yu, Katherine Brown |
CSHL 87th Symposium: Stem Cells
Preprints mentioned by speakers at the #CSHLsymp23
| List by | Alex Eve |
Journal of Cell Science meeting ‘Imaging Cell Dynamics’
This preList highlights the preprints discussed at the JCS meeting 'Imaging Cell Dynamics'. The meeting was held from 14 - 17 May 2023 in Lisbon, Portugal and was organised by Erika Holzbaur, Jennifer Lippincott-Schwartz, Rob Parton and Michael Way.
| List by | Helen Zenner |
9th International Symposium on the Biology of Vertebrate Sex Determination
This preList contains preprints discussed during the 9th International Symposium on the Biology of Vertebrate Sex Determination. This conference was held in Kona, Hawaii from April 17th to 21st 2023.
| List by | Martin Estermann |
Alumni picks – preLights 5th Birthday
This preList contains preprints that were picked and highlighted by preLights Alumni - an initiative that was set up to mark preLights 5th birthday. More entries will follow throughout February and March 2023.
| List by | Sergio Menchero et al. |
CellBio 2022 – An ASCB/EMBO Meeting
This preLists features preprints that were discussed and presented during the CellBio 2022 meeting in Washington, DC in December 2022.
| List by | Nadja Hümpfer et al. |
2nd Conference of the Visegrád Group Society for Developmental Biology
Preprints from the 2nd Conference of the Visegrád Group Society for Developmental Biology (2-5 September, 2021, Szeged, Hungary)
| List by | Nándor Lipták |
Fibroblasts
The advances in fibroblast biology preList explores the recent discoveries and preprints of the fibroblast world. Get ready to immerse yourself with this list created for fibroblasts aficionados and lovers, and beyond. Here, my goal is to include preprints of fibroblast biology, heterogeneity, fate, extracellular matrix, behavior, topography, single-cell atlases, spatial transcriptomics, and their matrix!
| List by | Osvaldo Contreras |
EMBL Synthetic Morphogenesis: From Gene Circuits to Tissue Architecture (2021)
A list of preprints mentioned at the #EESmorphoG virtual meeting in 2021.
| List by | Alex Eve |
EMBL Conference: From functional genomics to systems biology
Preprints presented at the virtual EMBL conference "from functional genomics and systems biology", 16-19 November 2020
| List by | Jesus Victorino |
Single Cell Biology 2020
A list of preprints mentioned at the Wellcome Genome Campus Single Cell Biology 2020 meeting.
| List by | Alex Eve |
Society for Developmental Biology 79th Annual Meeting
Preprints at SDB 2020
| List by | Irepan Salvador-Martinez, Martin Estermann |
FENS 2020
A collection of preprints presented during the virtual meeting of the Federation of European Neuroscience Societies (FENS) in 2020
| List by | Ana Dorrego-Rivas |
Planar Cell Polarity – PCP
This preList contains preprints about the latest findings on Planar Cell Polarity (PCP) in various model organisms at the molecular, cellular and tissue levels.
| List by | Ana Dorrego-Rivas |
Cell Polarity
Recent research from the field of cell polarity is summarized in this list of preprints. It comprises of studies focusing on various forms of cell polarity ranging from epithelial polarity, planar cell polarity to front-to-rear polarity.
| List by | Yamini Ravichandran |
TAGC 2020
Preprints recently presented at the virtual Allied Genetics Conference, April 22-26, 2020. #TAGC20
| List by | Maiko Kitaoka et al. |
3D Gastruloids
A curated list of preprints related to Gastruloids (in vitro models of early development obtained by 3D aggregation of embryonic cells). Updated until July 2021.
| List by | Paul Gerald L. Sanchez and Stefano Vianello |
ASCB EMBO Annual Meeting 2019
A collection of preprints presented at the 2019 ASCB EMBO Meeting in Washington, DC (December 7-11)
| List by | Madhuja Samaddar et al. |
EDBC Alicante 2019
Preprints presented at the European Developmental Biology Congress (EDBC) in Alicante, October 23-26 2019.
| List by | Sergio Menchero et al. |
EMBL Seeing is Believing – Imaging the Molecular Processes of Life
Preprints discussed at the 2019 edition of Seeing is Believing, at EMBL Heidelberg from the 9th-12th October 2019
| List by | Dey Lab |
SDB 78th Annual Meeting 2019
A curation of the preprints presented at the SDB meeting in Boston, July 26-30 2019. The preList will be updated throughout the duration of the meeting.
| List by | Alex Eve |
Lung Disease and Regeneration
This preprint list compiles highlights from the field of lung biology.
| List by | Rob Hynds |
Young Embryologist Network Conference 2019
Preprints presented at the Young Embryologist Network 2019 conference, 13 May, The Francis Crick Institute, London
| List by | Alex Eve |
Pattern formation during development
The aim of this preList is to integrate results about the mechanisms that govern patterning during development, from genes implicated in the processes to theoritical models of pattern formation in nature.
| List by | Alexa Sadier |
BSCB/BSDB Annual Meeting 2019
Preprints presented at the BSCB/BSDB Annual Meeting 2019
| List by | Dey Lab |
Zebrafish immunology
A compilation of cutting-edge research that uses the zebrafish as a model system to elucidate novel immunological mechanisms in health and disease.
| List by | Shikha Nayar |









 (No Ratings Yet)
(No Ratings Yet)